Jane Liang
Research Scientist at Kaiser Permanente Division of Research
Matrix Linear Models
Matrix linear models are a flexible and computationally efficient framework for detecting associations in structured high-throughput data. Examples of high-throughput data include:
- Measuring gene transcription on a genome-wide scale using microarrays.
- Screening a genetic mutant library under different growth conditions to analyze the effects of gene-condition interactions on colony size.
- Subjecting various cancer cells to a range of treatment drugs in order to identify genetic features targeted by particular therapies.
- Using mass spectrometry to detect levels of chemicals in human tissues.
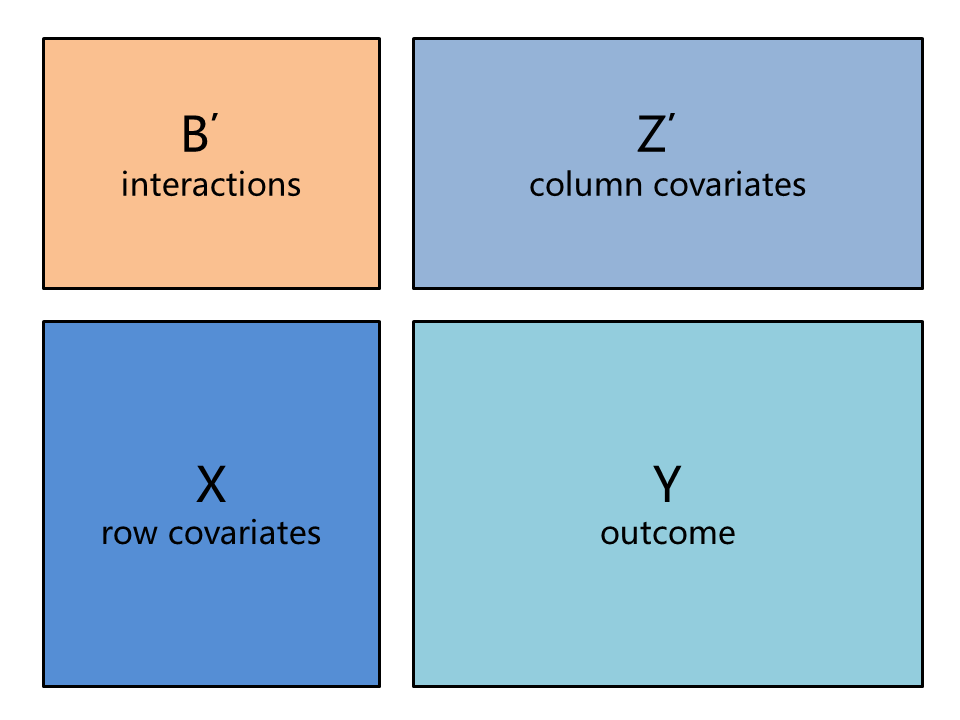
We developed closed-form least squares estimates applied to genetic screening data as well as sparse algorithms for estimating the interactions B. Our estimation methods are fast because we leverage matrix properties and the structure of the data. These methods are implemented in open-source code using the high-level programming language Julia, which combines ease of prototyping with computational speed.
We develop closed-form least squares estimates and demonstrate their ability to model relationships between mutants and conditions in genetic screening data. Matrix linear models can encode both categorical and continuous relationships to enhance detection of associations. We evaluate our method’s performance in simulations and in an Escherichia coli chemical genetic screen 1, comparing it with an existing univariate approach based on modified t-tests 2. We show that matrix linear models perform slightly better than the univariate approach when mutants and conditions are classified in nonoverlapping categories, and substantially better when conditions can be ordered in dosage categories.
Liang, J. W., Nichols, R. J., & Sen, Ś. (2019). Matrix linear models for high-throughput chemical genetic screens. Genetics, 212(4), 1063–1073. doi: 10.1534/genetics.119.302299.
MatrixLM.jl: Julia package with core functions to obtain closed-form least squares estimates for matrix linear models.
GeneticScreens.jl: Julia package that extends matrixLM.jl to provide pre- and post-processing for the analysis of high-throughput genetic screens using matrix linear models.
Supplemental code: Julia and R code used to analyze the results and reproduce the figures in the paper.
We induce sparsity in matrix linear models using an L1 penalty and consider the case when the response matrix and the covariate matrices are large. Standard methods for estimation of these penalized regression models fail if the problem is converted to the corresponding univariate regression problem, motivating our fast estimation algorithms (coordinate descent, FISTA, and ADMM) that utilize the structure of the model. Our method’s performance was evaluated on simulated data based on an environmental screening study 3 and two Arabidopsis thaliana genetic datasets with multivariate responses 4,5.
Liang, J. W. & Sen, Ś. (2022). Sparse matrix linear models for structured high-throughput data. The Annals of Applied Statistics, 16(1), 169-192. doi: 10.1214/21-aoas1444.
MatrixLMnet.jl: Julia package with core functions to obtain L1-penalized estimates for matrix linear models.
Supplemental code: Julia and R code used to analyze the results and reproduce the figures in the paper.
Lightning talk: Video recording of a talk I gave at JuliaCon 2017 in Berkeley, CA.
-
Nichols, R. J., Sen, S., Choo, Y. J., Beltrao, P., Zietek, M., Chaba, R., Lee, S., Kazmierczak, K. M., Lee, K. J., Wong, A., et al. (2011). Phenotypic landscape of a bacterial cell. Cell, 144(1):143–156. ↩
-
Collins, S. R., Schuldiner, M., Krogan, N. J., and Weissman, J. S. (2006). A strategy for extracting and analyzing large-scale quantitative epistatic interaction data. Genome biology, 7(7):R63. ↩
-
Woodruff, T. J., Zota, A. R., & Schwartz, J. M. (2011). Environmental chemicals in pregnant women in the United States: NHANES 2003–2004. Environmental health perspectives, 119(6), 878-885. ↩
-
Ågren, J., Oakley, C. G., McKay, J. K., Lovell, J. T., & Schemske, D. W. (2013). Genetic mapping of adaptation reveals fitness tradeoffs in Arabidopsis thaliana. Proceedings of the National Academy of Sciences, 110(52), 21077-21082. ↩
-
Lowry, D. B., Logan, T. L., Santuari, L., Hardtke, C. S., Richards, J. H., DeRose-Wilson, L. J., … & Juenger, T. E. (2013). Expression quantitative trait locus mapping across water availability environments reveals contrasting associations with genomic features in Arabidopsis. The Plant Cell, 25(9), 3266-3279. ↩